Gráfico do MRU

O movimento uniforme é o movimento onde a velocidade não varia com o tempo, isto é, a velocidade é constante.

Sabendo que a velocidade escalar média de um móvel pode ser dada por:

v = ΔS / Δt

Onde:
Δs = s – s₀ , é a variação do espaço, medida em metros (m)
Δt = t – t₀, é a variação do tempo, medida em segundos (s)

Fazendo o tempo inicial igual a zero (t0 = 0) temos:

v = (s – s₀) / t

Isolando o espaço final (s) na equação, temos que:

s = s₀ + v.t, v ≠ 0 (função horária do espaço no MU)

Podemos observar que o espaço é uma função do tempo s = f(t), do 1º grau em t.
Uma função de 1º grau é representada graficamente por uma reta, no sistema de coordenadas cartesianas, em relação ao eixo dos tempos.

Para v > 0 a função é crescente, assim o gráfico da função pode ser:

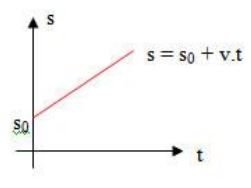
CINEMÁTICA ESCALAR – FÍSICA

Gráfico do MU para v = cte. > 0

Notamos que o gráfico da função é uma reta crescente, portanto, o movimento é progressivo, ou seja, o móvel caminha na mesma direção e sentido da orientação da trajetória.

Para v < 0 a função é decrescente, e a representação gráfica da função é:

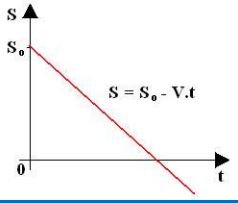
Gráfico do MU, para v = cte. < 0

Nesse caso a velocidade é menor do que zero (v < 0), o movimento é retrógrado, ou seja, o móvel caminha no sentido contrário ao da orientação da trajetória.

Gráficos da velocidade

Como a velocidade escalar média é constante, os gráficos podem ser:

1 – Para v > 0:

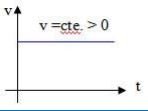
v > 0 – Movimento Progressivo

Note que o gráfico da velocidade é uma reta paralela ao eixo dos tempos, para v = f(t). Essa função é uma função constante.

2 – Para v < 0:

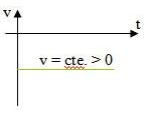
v < 0 – Movimento Retrógrado

Nota: Os gráficos não determinam a trajetória, apenas representam as funções do movimento.

Como no movimento uniforme a aceleração é nula (a = 0), o gráfico da aceleração é uma reta que coincide com o eixo dos tempos.

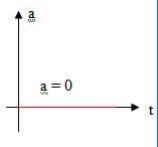
Gráfico da aceleração MU

* cte = constante