Sistema de Numeração e Conjunto dos Números Inteiros

O sistema de numeração foi desenvolvido para quantificar. Com o tempo, surgiu a necessidade de representar números menores que zero. Situações como medir a temperatura em regiões que nevam, estar em andares abaixo do solo (subsolo) ou representar o saldo de gols em partidas de futebol são exemplos do uso dos números negativos.

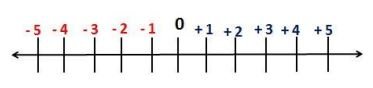
A Reta Numérica

O conjunto dos números inteiros é formado por números positivos, negativos e o zero. Esse conjunto é infinito nos dois sentidos da reta numérica.

Relação de Inclusão

A notação para representar o conjunto dos números inteiros é a letra Z. Há uma relação de inclusão entre os conjuntos:

N ⊂ Z

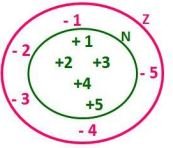
Exemplo de Inclusão:

• Elementos do conjunto N: {+1, +2, +3, +4, +5}
• Elementos do conjunto Z: {-5, -4, -3, -2, -1, 0, +1, +2, +3, +4, +5}

Observe que os números naturais (N) pertencem ao conjunto dos números inteiros (Z), por isso dizemos que N ⊂ Z.

Subconjuntos dos Números Inteiros

Conjunto dos Números Inteiros Não Negativos

Z⁺ = { x ∈ Z | x ≥ 0 }

Exemplo: Z⁺ = {0, +1, +2, +3, +4, +5 …}

Conjunto dos Números Inteiros Não Positivos

Z⁻ = { x ∈ Z | x ≤ 0 }

Exemplo: Z⁻ = { … -5, -4, -3, -2, -1, 0 }

Conjunto dos Números Inteiros Positivos Não Nulos

Z⁺* = { x ∈ Z | x > 0 }

Exemplo: Z⁺* = { +1, +2, +3, +4, +5 … }

Obs.: o asterisco (*) indica que o número zero não pertence ao conjunto.

Conjunto dos Números Inteiros Negativos Não Nulos

Z⁻* = { x ∈ Z | x < 0 }

Exemplo: Z⁻* = { … -5, -4, -3, -2, -1 }

Obs.: o asterisco (*) indica que o número zero não pertence ao conjunto.